Well, thật ra là không phải ăn một chiếc 🍩 thật. Mà là biến một chiếc bánh được viết bằng C thành một thứ ngầu như thế này


Đây là một đoạn code khá cũ. Được a1k0n viết từ tận năm 2011 cũng như đã có khá nhiều bài viết cũng như YouTube video giải thích thuật toán của bài này. Ví dụ như của Joma Tech hay mới đây nhất là Green Code. Mỗi bài đều có cách thể hiện khác nhau và đặt biệt là khá hài hước để bạn có thể ngồi xem và lắng nghe cách từng người giải thích thuật toán mà tôi khuyến khích bạn nên xem.
Quay lại với đoạn code trên. Thử chạy chương trình và xem kết quả. 🤔🤔 Hmm lỗi!!!
test.c:2:14: error: type specifier missing, defaults to 'int'; ISO C99 and later do not support implicit int [-Wimplicit-int]
2 | k;double sin()
| ^
| int
test.c:3:17: error: type specifier missing, defaults to 'int'; ISO C99 and later do not support implicit int [-Wimplicit-int]
3 | ,cos();main(){float A=
| ^
| int
test.c:5:12: error: call to undeclared library function 'printf' with type 'int (const char *, ...)'; ISO C99 and later do not support implicit function declarations [-Wimplicit-function-declaration]
5 | 1760];printf("\\x1b[2J");for(;;
| ^
test.c:5:12: note: include the header <stdio.h> or explicitly provide a declaration for 'printf'
test.c:6:5: error: call to undeclared library function 'memset' with type 'void *(void *, int, unsigned long)'; ISO C99 and later do not support implicit function declarations [-Wimplicit-function-declaration]
6 | ){memset(b,32,1760);memset(z,0,7040)
| ^
test.c:6:5: note: include the header <string.h> or explicitly provide a declaration for 'memset'
test.c:18:4: error: call to undeclared function 'putchar'; ISO C99 and later do not support implicit function declarations [-Wimplicit-function-declaration]
18 | putchar(k%80?b[k]:10);A+=0.04;B+=
| ^
À, 🥴. Tôi vừa quay lại sau khi học 1 khoá c cơ bản để có thể debug đống lỗi trên sau khi không dùng nó trong vài năm trời 😑. Đây là chương trình sau khi đã định dạng lại code và sửa lại hết tất cả các lỗi trên.
// a1k0n.c
#include <stdio.h>
#include <string.h>
#include <math.h>
int k;
int main()
{
float A = 0;
float B = 0;
float i, j;
float z[1760];
char b[1760];
printf("\\x1b[2J");
for (;;)
{
memset(b, 32, 1760);
memset(z, 0, 7040);
for (j = 0; 6.28 > j; j += 0.07)
for (i = 0; 6.28 > i; i += 0.02)
{
float c = sin(i);
float d = cos(j);
float e = sin(A);
float f = sin(j);
float g = cos(A);
float h = d + 2;
float D = 1 / (c * h * e + f * g + 5);
float l = cos(i);
float m = cos(B);
float n = sin(B);
float t = c * h * g - f * e;
int x = 40 + 30 * D * (l * h * m - t * n);
int y = 12 + 15 * D * (l * h * n + t * m), o = x + 80 * y, N = 8 * ((f * e - c * d * g) * m - c * d * e - f * g - l * d * n);
if (22 > y && y > 0 && x > 0 && 80 > x && D > z[o])
{
z[o] = D;
b[o] = ".,-~:;=!*#$@"[N > 0 ? N : 0];
}
}
printf("\\x1b[H");
for (k = 0; 1761 > k; k++)
{
putchar(k % 80 ? b[k] : 10);
}
A += 0.04;
B += 0.02;
}
return 0;
}
Chạy thử chương trình trên:
gcc -o a1k0n a1k0n.c
./a1k0n
Sau khi chạy chương trình thì đã ra được kết quả đúng, truy nhiên việc hiện thị bánh donut với tốc độ quay hơi nhanh (siêu nhanh). Để giảm tốc độ render donut, bạn có thể sử dụng hàm usleep(15000) từ thư viện <unistd.h> để làm việc render mượt mà hơn.
Và bùm .. So cool!! 😎 🔥🔥
Ngầu đét. Sau khi chạy chương trình thành công thì đã đến lúc ta đi sâu vào thuật toán của nó. Và bùm .. sốc phần 2 🤨. Dây là những gì tôi thấy sau khi lần đầu tiên lướt qua bài phân tích của A1k0n.

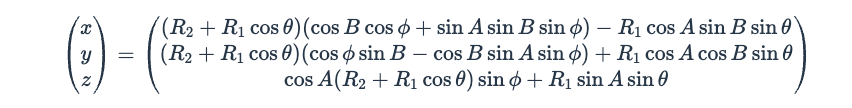
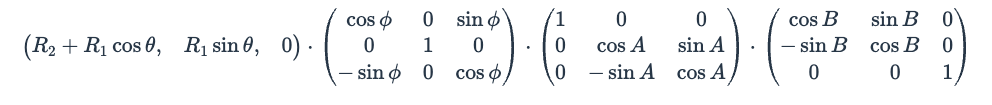
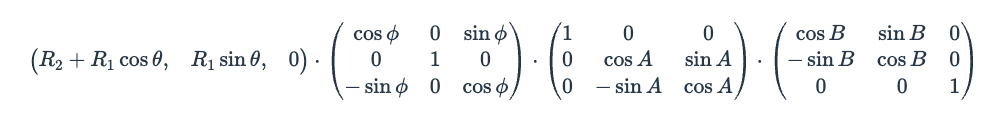
Và đây là những gì đọng lại…. 🥴 nothing.
Bỏ qua nó :v. Sau vài tiếng ngồi lại và thử nghiệm với các bài toán từ đơn giản đến phức tạp. Tôi viết bài này với mục đích chia sẻ lại cách mà tôi đã làm để hiểu rõ bài toán cũng như áp dụng những kiến thức đó để giải các bài toán khác.
Bài toán
Tưởng tự với ví dụ ở phần giới thiệu trên. Phần dưới sẽ mô tả lại quá trình giải bài toán hiện thì hình chiếc bánh donut ở dạng 3D trên terminal.
Trong bài hướng dẫn này, ta sử dụng chung 1 số hằng số.
// constant.h
#ifndef CONSTANT_H
#define CONSTANT_H
// Chiều rộng của terminal
#define SCREEN_WIDTH 80
// Chiều cao của terminal
#define SCREEN_HEIGHT 22
// Kích thước của terminal ( SCREEN_WIDTH * SCREEN_HEIGHT)
// 80 x 22
#define BUFFER_SIZE 1760
// 360deg
#define M_2PI 6.28
// Bước lặp với các góc
#define A_SPACING 0.07
#define B_SPACING 0.02
// Toạ dộ tâm của terminal
#define CENTER_X SCREEN_WIDTH / 2
#define CENTER_Y SCREEN_HEIGHT / 2
#endif // CONSTANT_H
Hiện thị chiếc bánh donut đơn giản trên không gian 2D
Mục tiêu của bài toán này là giúp bạn làm quen với việc biểu diễn một biểu thức toán học bằng ngôn ngữ C.
Cho hằng số R1 và R2 với R2 > R1. Yêu cầu vẽ phần diện tích ở giữa 2 đường tròn này.
Phương trình tập hợp các điểm thuộc vành khuyên trên trong toạ độ cực:
$$ (x,\ y) = (r\cos\alpha,\ r\sin\alpha) $$
Với điều kiện:
$$ R_1 \leq r \leq R_2, \quad 0 \leq \alpha < 2\pi $$
Chương trình C hiện thị vành khuyên theo công thức trên:
// simple2Ddonut.c
#include <stdio.h> // For printf and putchar
#include <string.h> // For memset
#include <math.h> // For sin and cos
#include "constant.h"
const int R1 = 4;
const int R2 = 10;
void renderDonut() {
float alpha;
// Tạo một mảng buffer lưu lại giá trị được hiện thị ở vị trí (x, y) pixel trên
// terminal. Giá trị tại (x, y) được lưu ờ b[x + y * SCREEN_WIDTH]
char b[BUFFER_SIZE];
// clear terminal
printf("\\x1b[2J");
// chuyển đổi các ký tự trong buffer thành khoảng trắng
memset(b, 32, BUFFER_SIZE);
for (alpha = 0; alpha < M_2PI; alpha += A_SPACING ) {
for (int R = R1; R < R2; R += 1) {
int x = CENTER_X + (int)round(R * cos(alpha));
int y = CENTER_Y + (int)round(R * sin(alpha));
int o = x + SCREEN_WIDTH * y;
if (y < SCREEN_HEIGHT && y > 0 && x > 0 && SCREEN_WIDTH > x ) {
b[o] = '.';
}
}
}
for (int k = 0; k <= BUFFER_SIZE; k++)
{
putchar(k % SCREEN_WIDTH ? b[k] : 10);
}
}
int main() {
renderDonut();
return 0;
}
kết quả:
.......
...........
.............
............. .
.................
.................
........ ........
....... .......
...... ......
...... ......
...... ......
....... .......
....... .......
.................
.................
...............
.............
..........
.......
Bài toàn này được đưa ra nhằm mục đích giới thiệu và làm quen việc hiện thị vành khuyên trên terminal. Việc hiện thị bánh donut cũng sẽ tương tự như trên.
Tìm hiểu công thức toán học của chiếc bánh Donut
Gọi là bánh donut thôi chứ thật ra nó là một hình hình xuyến (Torus) là một bề mặt xoay (Solid of revolution) được tạo thành bằng cách xoay một vòng tròn trong không gian 3 chiều quanh một trục đồng phẳng với hình tròn.
Định nghĩa trông có vẻ khó hiểu, tôi sẽ giải thích chi tiết hơn thông qua các biểu thức toán học và hỉnh ảnh bên dưới.
Đầu tiên là vẽ một hình tròn có bán kinh là R1 với tâm tại (R2, 0, 0) trong mặt phẳng (x, y) tương tư như trên.
$$ (x,\ y,\ z)=(R_2, \ 0,\ 0)+(R_1 \cos \theta,\ R_1\sin \theta,\ 0) \\ \ \ \ \ = (R_2 + R_1 \cos \theta,\ R_1\sin \theta, \ 0)
$$
Với điều kiện:
R_1 < R_2,\quad 0 \leq \theta < 2\pi $$
Sau đó thực hiện
quay hình tròn này quanh trục y từ 0 đến 2***π.*** Ta thực hiện việc quay bằng cách nhân phương trình hình tròn trên với ma trận quay (Rotation matrix) với trục quay y.
Ma trận quay quay trục y:
$$ R_y(\phi) = \begin{bmatrix} \cos\phi & 0 & -\sin\phi \\ 0 & 1 & 0 \\ \sin\phi & 0 & \cos\phi \end{bmatrix} \\ $$
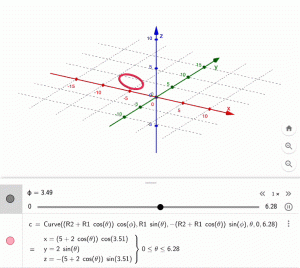
Phương trình kết quả sau khi nhân với ma trận xoay quanh trục y:
$$ (R_2 + R_1\cos\theta,\ R_1\sin\theta,\ 0) \cdot
\begin{bmatrix} \cos\phi & 0 & -\sin\phi \\ 0 & 1 & 0 \\ \sin\phi & 0 & \cos\phi \end{bmatrix} \\ = ((R_2 + R_1\cos\theta)\cos\phi, \ R_1\sin\theta,\ -(R_2 + R_1\cos\theta)\sin\phi) $$
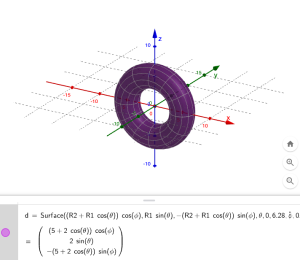
Như vậy ta đã có được hình ảnh chiếc Donut trong không gian 3 chiều. Để đạt được kết quả như đề ra. ta thực hiện xoay quanh 2 trục còn lại x, z tương tự như với trục y.
Ma trận quay quanh trục x, z tương ứng là:
$$
R_x(A) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos A & \sin A\\ 0 & -\sin A & \cos A \end{bmatrix} \\ \\
R_z(B) = \begin{bmatrix} \cos B & \sin B & 0 \\ -\sin B & \cos B & 0 \\ 0 & 0 & 1 \end{bmatrix} \\
((R_2 + R_1\cos\theta)\cos\phi, \ R_1\sin\theta ,\ -(R_2 + R_1\cos\theta)\sin\phi) \cdot R_x(A) \cdot R_z(B)
$$
Sau khi thực hiện phép nhân trên ta được kết quả:
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix}
\begin{pmatrix} (R_2 + R_1 \cos \theta)(\cos B \cos \phi + \sin A \sin B \sin \phi) – R_1 \cos A \sin B \sin \theta \\ (R_2 + R_1 \cos \theta)(\cos \phi \sin B – \cos B \sin A \sin \phi) + R_1 \cos A \cos B \sin \theta \\ \cos A (R_2 + R_1 \cos \theta) \sin \phi + R_1 \sin A \sin \theta \end{pmatrix} $$
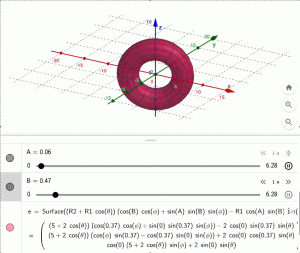
Như được thể hiện trong hình trên. Ta đã thu được phương trình toán học cho bài toán quay hình xuyến trong không gian 3 chiều.
Như các bạn để ý. mặt phẳng của terminal là mặt phẳng 2 chiều. Vậy làm thể nào để hiện thị hình xuyến trên? Câu hỏi đó dẫn đến bài toán tiếp theo.
Phép chiếu vật thể 3 chiều lên không gian 2 chiều
Phép Chiếu phối cảnh (Perspective Projection)
Phép chiếu phối cảnh là phương pháp chiếu một điểm từ không gian 3 chiều (3D) lên mặt phẳng 2 chiều (2D) sao cho vật thể gần thì lớn, xa thì nhỏ — tạo cảm giác chiều sâu chân thực như mắt người nhìn.
Công thức chiếu phối cảnh đơn giản
Khi mắt đặt ở gốc và nhìn dọc theo trục Z, thì phép chiếu phối cảnh được mô tả bằng công thức:
$$ x’ = \frac{z’ \cdot x}{z}\ ; \ y’ = \frac{z’ \cdot y}{z}\ $$
Giải thích:
x,y,z: tọa độ gốc của điểm 3D.z': khoảng cách từ mắt đến mặt phẳng chiếu.x',y': tọa độ điểm chiếu 2D.
Kết quả: điểm nào có z lớn (xa mắt) sẽ có x, y nhỏ nhằm tạo hiệu ứng vật thể nhỏ đi khi ở xa.
Trong bài hướng dẫn này, z' là cố định. Chúng ta đặt nó là K1 . Giá trị này phụ thuộc vào vật thể ta mong muốn chiếu lên mặt phẳng 2 chiều.
Ví dụ đối với các hằng số trong bài toán này. Chúng ta có mặt phẳng với 80 x 22 pixels và vật thể được chiếu tại tâm của mặt phẳng (40, 21). Chúng ta muốn xem một vật thể có chiều rộng 10 đơn vị và cách 5 đơn vị từ người xem. Chúng ta chọn K1 sao cho việc chiếu vật thể tại x = 10 và z=5 vẫn trong không gian của terminal.
$$ x’ < screen\_width/2 \\ \frac{K_1 \cdot x}{z} < 40\\ K_1 < 20 $$
Vấn đề là khi chiếu một vật từ không gian 3 chiều lên mặt phẳng 2 chiều. Ta sẽ gặp một số trường hợp các điểm (x, y , z) khác nhau nhưng sau khi chiếu ra thì (x’, y’) là giống nhau. Để phân biệt 2 điểm này. Ta sẽ lưu lại giá trị
$$ z^{-1} = \frac{1}{z} $$
của bất cứ điểm nào ta vẽ, Khi vẽ một điểm nào mới trên màn hình, ta trước tiên kiểm tra xem nó đã tồn tại hay chưa. Chúng ta chỉ vẽ một điểm khi giá trị trên lớn hơn đồng nghĩa với điểm được vẽ ngần màn hình hơn.
Ở trong phần trước, ta có thể thấy hình xuyến đang được xoay quanh tâm (0, 0,0). Để có thể nhìn rõ hơn trong mặt phẳng 2 chiều, ta thực hiện đẩy lùi hình xuyến về trục Z thêm 1 khoảng K2 . Vì vậy công thức chiếu cuối cùng là
$$ x’ = \frac{K1 \cdot x}{z + K2}\ ; \ y’ = \frac{K1 \cdot y}{z + K2}\ $$
Hiện thị chiếc bánh donut 3 chiều
Chúng ta đã đi qua một số biểu thức và lý thuyết, cùng áp dụng nó để biểu thị thông qua code C
// 3DDonutIgnoreDepth.c
#include <stdio.h> // For printf and putchar
#include <math.h> // For sin and cos
#include <string.h> // For memset
#include <unistd.h> // For usleep
#include "constant.h"
const int K1 = 15;
const int K2 = 6;
const int R1 = 1;
const int R2 = 3;
void renderDonut()
{
float A = 0;
float B = 0;
char b[BUFFER_SIZE];
float z[BUFFER_SIZE];
// Clear the screen
printf("\\x1b[2J");
for (;;)
{
memset(b, 32, BUFFER_SIZE);
memset(z, 0, BUFFER_SIZE * 4);
for (float phi = 0; phi < M_2PI; phi += A_SPACING) {
for (float theta = 0; theta < M_2PI; theta += B_SPACING)
{
float crx = R2 + R1 * cos(theta);
float cry = R1 * sin(theta);
float cp = cos(phi);
float sp = sin(phi);
float cA = cos(A);
float sA = sin(A);
float cB = cos(B);
float sB = sin(B);
float D = cA * crx * sp + cry * sA; // z
float score = 1 / (D + K2);
int x = CENTER_X + K1 * score * (crx * (cB * cp + sA * sB * sp) - cry * cA * sB);
int y = CENTER_Y + K1 * score * (crx * (cp * sB - cB * sA *sp) + cry * cA * cB);
int o = x + SCREEN_WIDTH * y;
// // The donut is represented as a series of ASCII characters, and the character to be printed is determined by the value of N.
if (y < SCREEN_HEIGHT && y > 0 && x > 0 && SCREEN_WIDTH > x && score > z[o])
{
z[o] = score;
b[o] = '.';
}
}
}
printf("\\x1b[H");
for (int k = 0; k <= BUFFER_SIZE; k++)
{
putchar(k % SCREEN_WIDTH ? b[k] : 10);
}
usleep(15000);
A += A_SPACING;
B += B_SPACING;
}
}
int main()
{
renderDonut();
return 0;
}
// gcc -o 3DDonutIgnoreDepth 3DDonutIgnoreDepth.c
// ./3DDonutIgnoreDepth
Sau khi build và chạy thử chương trình trên ta được kết quả:
Bằng cách thay đổi các tham số R1 , R2 , K1 , K2 để có thể phóng to, thu nhỏ, mở rộng.. chiếc bánh donut trên. Ngoài ra bạn có thể thay đổi vòng lặp để thu được một vài kết quả thú vị khác.
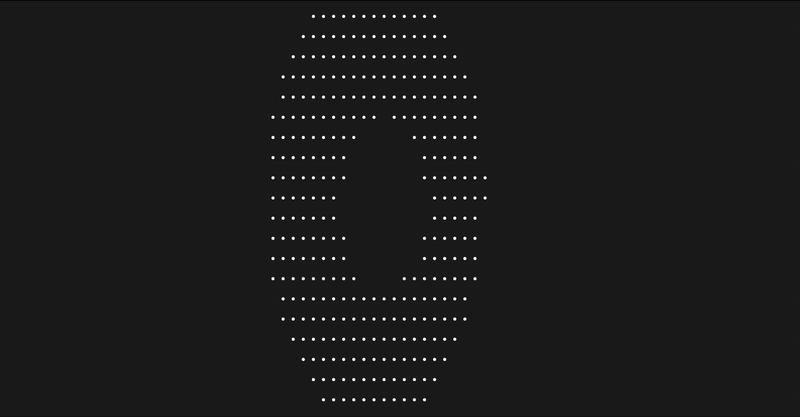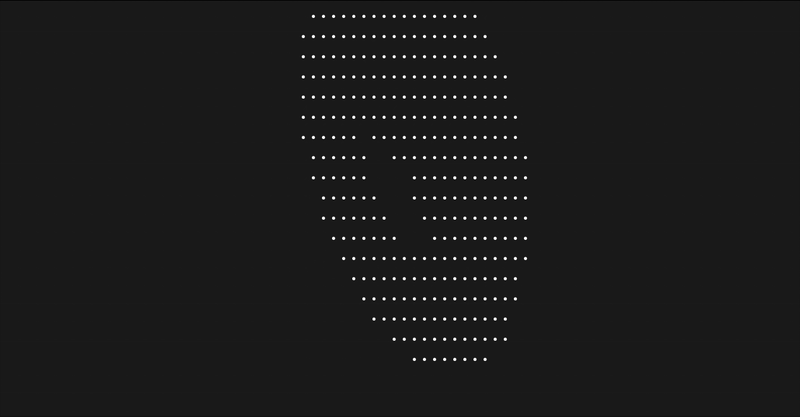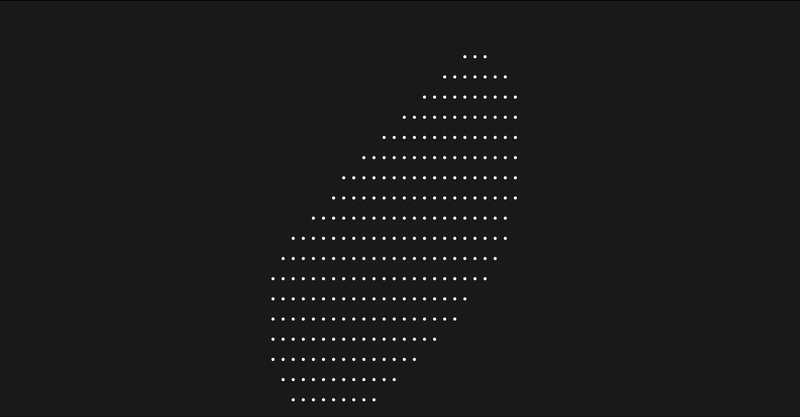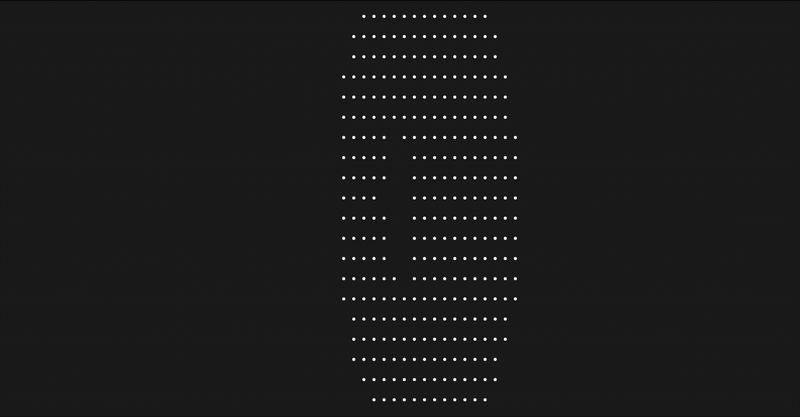
Thể hiện độ sáng tối
Qua phần trên chúng ta đã thể hiện được chiếc bánh donut trên màn hình. Tuy nhiên mỗi điểm của chiếc bánh chỉ được thể thiện bằng kí tự . rất đơn điệu và khác xa với bản gốc.
Để thể hiện đổ sáng tối của vật thể, ngoài việc tính toán vị trí của nó trên màn hình, chúng ta cần tính toán xem điểm đó có đang quay mặt về phía ánh sáng hay không.
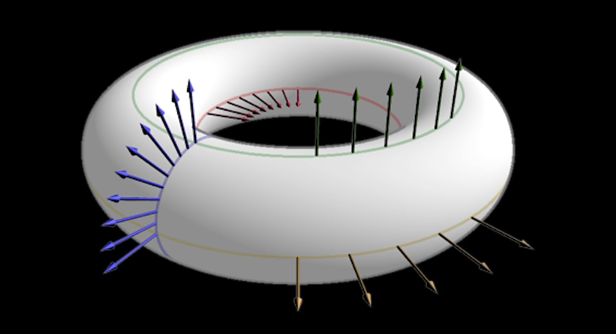
Để tính toán độ chiếu sáng, chúng ta cần biết vector pháp tuyến (surface normal) – hướng vuông góc với bề mặt tại mỗi điểm. Sau đó chúng ta tính tích vô hướng (dot product) của vector pháp tuyến ấy với hướng của ánh sáng. Nếu tích vô hướng > 0 thì về mặt đó hướng về phía ánh sáng, ngược lại nếu < 0 thì bề mặt hướng ra xa ánh sáng. Giá trị càng lớn thì độ sáng càng cao.
Phép suy ra hướng pháp tuyến bề mặt hóa ra khá giống với phép suy ra điểm trong không gian. Chúng ta bắt đầu với một điểm trên một đường tròn, xoay nó quanh trục trung tâm của hình xuyến, rồi thực hiện thêm hai phép quay nữa. Pháp tuyến bề mặt của điểm trên đường tròn khá rõ ràng: nó giống với điểm trên một đường tròn đơn vị (bán kính R1= 1) có tâm tại gốc tọa độ.
Vì vậy, pháp tuyến bề mặt của chúng ta N được suy ra giống như trên.
Ban đầu, lấy 1 điểm trên vòng tròn nhỏ của hình xuyến
$$ (\cos\theta,\ \sin\theta,\ 0) $$
Đây chính là vector pháp tuyến của hình tròn con. Bình thường điểm đó sẽ nằm yên, nhưng hình xuyến của ta được xoay đều quanh 3 trục. Nên ta phải xoay nó tương tự như với hình xuyến. Vì vậy công thức của N sẽ được viết lại là:
$$ (N_x,\ N_y,\ N_z) = (\cos\theta,\ \sin\theta,\ 0) \cdot R_y(\phi) \cdot R_x(A) \cdot R_z(B) $$
https://www.youtube.com/watch?v=sW9npZVpiMI
Chúng ta đã có công thức của vector pháp tuyến của mỗi điểm trên bề mặt hình xuyến, thế còn nguồn sáng thì sao. Bạn có thể chọn một nguồn sáng khác, tuy nhiên trong bài viết này t chọn nguồn sáng như của tác giả (0, 1, -1) .Đây là ánh sáng chiếu từ trên đầu và từ phía sau người xem.
Tính độ sáng (luminance)
$$ L = (N_x,\ N_y,\ N_z) \cdot (0,\ 1,\ -1) = N_y – N_z \\ = \cos\phi\cos\theta\sin B-\cos A\cos\theta\sin\phi-\sin A\sin\theta+\cos B(\cos A\sin\theta-\cos\theta\sin A\sin\phi) $$
Và nếu L > 0 thì chỗ mặt đó được hứng sáng, ngược lại mặt đó bị tối. Vậy làm thế nào để thể hiện độ sáng trên màn hình. Ta thực hiện chuyển đổi các giá trị của L thành các giá trị ASCII tương ứng .,-~:;=!*#$@ từ tối cho đến sáng nhất.
| Luminance (L) | Ký tự |
|---|---|
| 1 | . |
| 2 | , |
| 3 | – |
| 4 | ~ |
| 5 | : |
| 6 | ; |
| 7 | = |
| 8 | ! |
| 9 | * |
| 10 | # |
| 11 | $ |
| 12 | @ |
Vì giá trị của L chỉ từ [0...√2] nên ta cần nhân với 8 để L sẽ nằm trong khoảng giá trị [0...12] để phù hợp với bảng trên.
Áp dụng công thức này và đưa vào đoạn code hiện thị bánh donut 3 chiều bên trên:
// ...
// Tinh toán độ sáng tối
int L = 8 * (cp * ct * sB - cA * ct * sp - sA * st + cB * (cA * st - ct * sA * sp));
if (y < SCREEN_HEIGHT && y > 0 && x > 0 && SCREEN_WIDTH > x && score > z[o])
{
z[o] = score;
// chuyển đổi thành các kí tự tương ứng
b[o] = ".,-~:;=!*#$@"[L > 0 ? L : 0];
}
// ...
Ta thu được kết quả:

Tổng kết
Chúng ta có áp dùng được bài này vào vấn đề thực tế không. Tất nhiên là không nhưng nó ngầu. 😙😙. Ngoài ra đây là bài toán cơ bản và được giới thiệu rất nhiều trong đồ hoạ máy tính. Tôi nghĩ bài viết đã đủ dài và cũng khá nhiều công thức toán học trong này. Nên tôi quyết định dừng lại tại đây, thêm vào đó tôi cũng có 1 số ý tưởng về việc việc áp dụng các kiến thức mình tổng hợp được để thực hiện nhiều thứ khác. Như vẽ hình khối, tam giác hay là thêm tương tác vào vật thể chứ không chỉ hiện thị trên terminal chẳng hạn.
Liên kết
- https://www.a1k0n.net/2011/07/20/donut-math.html: Bài viết của a1k0n, chủ nhân của đoạn code C.
- https://www.geogebra.org/m/nhwe4xhd: Hiện thị các công thức toán học trên không gian 3 chiều.
- https://www.youtube.com/watch?v=sW9npZVpiMI: Bài giải thích của Joma Tech
- https://www.youtube.com/watch?v=74FJ8TTMM5E: Bài giải thích của Green Code.
- https://en.wikipedia.org/wiki/3D_projection#Perspective_projection: Phép chiếu phối cảnh
 14 phút để đọc
14 phút để đọc

