Tìm chuỗi con Palindrome dài nhất trong Java [Hướng dẫn chi tiết]

Reading Time: 3 minutes

Tìm chuỗi con palindrome dài nhất là một câu hỏi phỏng vấn Java rất phổ biến. Để giải quyết bài toán này, trước tiên chúng ta cần xác định được thuật toán phù hợp cho nó.

Thuật toán tìm chuỗi con Palindrome dài nhất

Điểm mấu chốt ở đây là một chuỗi palindrome luôn đối xứng qua điểm tâm chính giữa của nó. Nếu ta xuất phát từ tâm và di chuyển dần ra hai phía, các ký tự ở vị trí đối xứng sẽ luôn giống nhau.

Ví dụ, chuỗi 12321 có tâm là 3. Nếu di chuyển ra hai bên, ta sẽ lần lượt gặp cặp ký tự 2 và 1.

Ta sẽ áp dụng logic này vào chương trình Java để tìm ra chuỗi con palindrome dài nhất. Tuy nhiên, khi một chuỗi palindrome có thể có độ dài chẵn, tâm của nó sẽ gồm hai ký tự. Vì vậy, chương trình của ta cũng cần xử lý trường hợp này.

Ví dụ, với chuỗi 12333321, tâm sẽ là 33. Nếu ta di chuyển ra hai biên từ tâm này, ta sẽ lần lượt gặp các cặp ký tự 3, 2, và 1.

Chương trình Java tìm chuỗi con Palindrome dài nhất

Trong chương trình Java ở dưới, ta sẽ duyệt qua từng ký tự của chuỗi đầu vào, coi mỗi ký tự (hoặc cặp ký tự) là một điểm tâm tiềm năng và từ đó mở rộng ra hai bên để kiểm tra dần dần. Ta sẽ dùng hai biến để lưu vị trí bắt đầu và kết thúc của chuỗi palindrome dài nhất tìm được cho đến hiện tại.

Vì một chuỗi có thể chứa chuỗi con nhiều palindrome, ta cũng cần so sánh và cập nhật kết quả mỗi khi tìm thấy một palindrome dài hơn. Dưới đây là chương trình hoàn chỉnh có thể hoạt động chính xác trong mọi trường hợp.

package com.journaldev.util;

public class LongestPalindromeFinder {

	public static void main(String[] args) {
		System.out.println(longestPalindromeString("1234"));
		System.out.println(longestPalindromeString("12321"));
		System.out.println(longestPalindromeString("9912321456"));
		System.out.println(longestPalindromeString("9912333321456"));
		System.out.println(longestPalindromeString("12145445499"));
		System.out.println(longestPalindromeString("1223213"));
		System.out.println(longestPalindromeString("abb"));
	}

	static public String intermediatePalindrome(String s, int left, int right) {
		if (left > right) return null;
		while (left >= 0 && right < s.length()
				&& s.charAt(left) == s.charAt(right)) {
			left--;
			right++;
		}
		return s.substring(left + 1, right);
	}

	// O(n^2)
	public static String longestPalindromeString(String s) {
		if (s == null) return null;
		String longest = s.substring(0, 1);
		for (int i = 0; i < s.length() - 1; i++) {
			//odd cases like 121
			String palindrome = intermediatePalindrome(s, i, i);
			if (palindrome.length() > longest.length()) {
				longest = palindrome;
			}
			//even cases like 1221
			palindrome = intermediatePalindrome(s, i, i + 1);
			if (palindrome.length() > longest.length()) {
				longest = palindrome;
			}
		}
		return longest;
	}

}

Còn đây là kêt quả khi ta chạy nó.

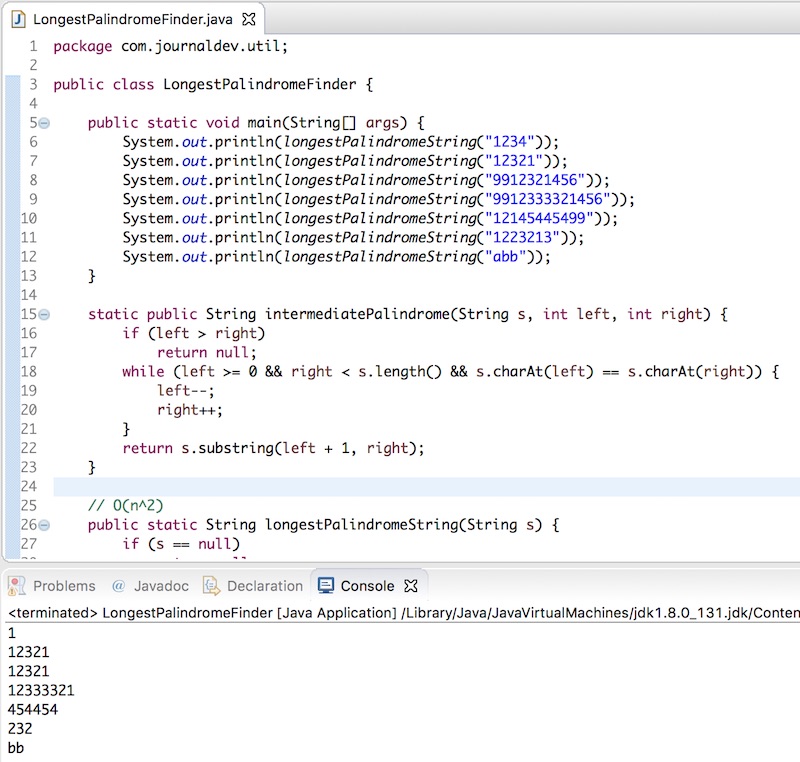
Ta có thể cải tiến code trên bằng cách tách logic kiểm tra và cập nhật kết quả ra một hàm riêng. Tuy nhiên, chúng tôi chủ đích để lại phần này cho bạn. Hãy cho chúng tôi và mọi người biết nếu bạn có cách triển khai nào tốt hơn hoặc phát hiện code chạy sai trong trường hợp nào đó.

Bạn có thể tải về toàn bộ code ví dụ từ link GitHub này.